Velocity-Profile Deviations Influence Flowmeter Performance
Selecting the right flowmeter for the liquid
By Corte Swearingen
Reprinted from Chemical Processing magazine
Close your eyes and imagine a world in which all fluids flowing down pipes are perfectly homogeneous, having no disturbances or eddies in the flow stream. A world in which pipes always contain fully developed turbulent flow and pipe bends and obstructions are non-existent.
Sounds silly right? But these are the hypothetical conditions upon which flowmeter accuracies are based. If deviations from these conditions exist, accuracy and/or repeatability will degrade. This article will discuss the first of four major influence quantities that affect flowmeter accuracy and performance: velocity-profile deviations, non-homogenous flow, pulsating flow, and cavitation. With this background, we will then look at how these influence quantities factor into flowmeter performance and what can be done to minimize their effect.
Imagine a horizontal pipe a few feet in front of you at about eye level. If a vertical cut were made through the center of the pipe to remove the front half of the pipe, it would be easy to see how "nicely behaved" fluid flow develops.
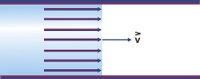
Figure 1: Zero Liquid Viscosity In the hypothetical situation shown here, the liquid viscosity is zero, and the velocity profile is a straight line. The vertical sheet of fluid moves forward at velocity V.
The cross-sectional view shown in Figure 1 illustrates a hypothetical situation in which the fluid has zero viscosity. In this example, the velocity gradient is constant and equal across the entire cross-section. That is, the fluid velocity at the pipe walls is equal to the fluid velocity at the pipe center and at all points in-between. However, every liquid has some measure of viscosity; therefore, the velocity profile becomes distorted from this "ideal case scenario."
Newtonian Velocity Profiles
Examples of Newtonian fluids include water, milk, sugar solutions and mineral oils. Distortions can occur for homogeneous Newtonian fluids for a number of reasons. The viscosity of a Newtonian fluid is dependent only on temperature, but not on shear rate and time. The flow of a Newtonian fluid will exhibit a "sticking" effect on the walls of the pipe. In fact, the boundary conditions placed on the stationary pipe wall demand that the fluid in direct contact with the pipe walls have zero velocity (or at least that is what is assumed in the calculations within this article). It is this boundary condition that distorts a Newtonian fluid's velocity profile.
If the velocity vector at the pipe wall is zero, the maximum velocity occurring in the pipe can be worked out mathematically.
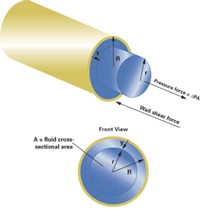
Figure 2: Sample Newtonian Fluid Velocity Profile For steady flow in a pipe of radius "R" containing a smaller cylindrical element of liquid radius "r," a shear force develops equal and opposite to the cylindrical water element pressure.
Consider a pipe of radius "R" that contains a smaller cylindrical element of liquid of radius "r." See Figure 2.
Assuming the cylindrical element of fluid is moving uniformly through the pipe, at constant velocity, the shearing force on the pipe wall is equal to the pressure force of the liquid moving through. The shear force, which is directly proportional to the velocity gradient, is given by:
τ = μ(dv/dy)
where: τ is the shear force or shear pressure.
dv/dy is the velocity gradient (where y is the distance from the pipe wall). μ is the constant of proportionality, also referred to as the dynamic viscosity.
Because the fluid pressure can be simply given as the pressure differential through the pipe times the cross-sectional fluid area, and because the fluid pressure force is equal to the oppositely directed shear force on the pipe wall, the equation can be written:
Shear Wall Force = τ(2πr)L = 2πrLμ(dv/dy) = ΔPA = ΔPπr2 = Fluid Pressure
where:
r is the radius of the cylindrical fluid element.
L is the length of the cylindrical fluid element.
ΔP is the pressure differential through the pipe.
A is the cross-sectional area of the fluid element
Solving for τ, we get
τ = ΔPr/2L
It is more convenient in this example to give the shear force as a function of the pipe center instead of the pipe wall. This is easily accomplished easily by rewriting the shear force as:
τ = -μ(dv/dr) = μ(dv/dy)
Equating these two expressions for the shear stress τ gives us the following relationship:
ΔPr/2L = -μ(dv/dr)
Solving for the velocity gradient yields:
dv/dr = -ΔPr/2μL
By integrating this expression across the pipe to radius R, the velocity (V) as a function of the radius r can be determined.
V = ΔP/4μL(R2 - r2)
Now it can be seen mathematically that the maximum velocity in the pipe occurs at the center of the pipe, or when r = 0. Actually, these two facts that the velocity at the pipe wall is zero and the maximum velocity occurs at the pipe center are the boundary conditions used to determine the constant of proportionality for the above integration.
This equation is in the form of a parabola. Graphing it gives the velocity profile shown in Figure 3.



